拾珍丨平遥镇国寺万佛殿大木结构测量数据解读

在前人对万佛殿大木结构实测及所绘制的相关图纸的基础上，清华大学综合运用全站仪、三维激光扫描仪和手工测量对这座重要的早期木结构进行了精细测绘工作。通过现有数据的分析，本文初步推算出古代匠人在万佛殿大木尺寸设计中采用了306毫米的营造尺，进一步分析了大木尺度设计的基本方法，讨论了该建筑的平面丈尺、斗栱、屋架等设计细节问题，并借助木材与碳同位素检测对建筑始建年代和遗存现状进行了分析与证实。

平遥镇国寺万佛殿大木结构测量数据解读

刘畅刘梦雨王雪莹

图1 平遥镇国寺总平面示意图及坐标测点位置

镇国寺位于平遥县城东北14公里襄垣乡的郝洞村，北纬37度17.119分，东经112度16.261分，海拔高度753米（坐标位置点参见图1）。镇国寺建筑群坐北向南，寺院规模前后两进院落，从南到北依次有天王殿、钟鼓二楼、前院东西二组配房、万佛殿及东西侧门、后院东配殿观音殿、西配殿地藏殿、东厢房、西厢房、三佛殿及其东西经、西配院玉皇阁遗址。万佛殿是镇国寺建筑群的主殿，位于院落中央，是一座面阔三间、进深三间的歇山顶建筑。根据殿内题记，可知万佛殿肇自北汉天会七年（963年），金代天德三年岁次辛未七月补修，明代嘉靖十九年（1540年）再次修缮，并将原名京城寺更名为今天的寺名镇国寺。天王殿内的题记则主要是乾隆时代所成，未能全面记录天王殿修缮历史。寺内现存碑刻20通，铸铁古钟一座。参考现存碑文、钟铭和其他古建筑上的题迹，可以判断镇国寺经历了金、明、清历代修葺，亦有碑记提到元代修缮之可能。

2010年以来，清华大学针对万佛殿和天王殿开展了精细测绘工作，结合手工测量和三维激光扫描实测，尝试开展统计分析，推导大殿原始设计的丈尺规律。

现有研究

到目前为止，关于万佛殿建筑史专业研究成果不多，调查中仅发现地方研究力量的一些工作：其一，山西古建筑研究所进行过比较深入的调查，而公开资料非常有限；其二，平遥县文物管理所绘制了一整套较完整的测绘图，而图中所标注数据存在精度不足的现象，亦未能全面公布。同时，前人关于万佛殿的认识主要反映在木结构研究和殿内彩塑壁画的介绍上，未能形成综合研究。

首先，万佛殿木结构被基本认定为始建于北汉天会七年（963年）。根据以往的实测，斗栱总高1.74米，斗栱的分布有柱头、补间和转角三种，补间斗栱每间一攒，五铺作，双杪偷心造。柱头斗栱七铺作双杪下昂重栱偷心造，昂为批竹式，耍头为短促的下昂形。铺作出跳1.43米，材高22厘米，宽16厘米，栔高10厘米，相当宋《营造法式》四等材标准。

具体到细节问题，前辈学者更有以下数据统计：

表1 万佛殿斗栱用材数据（单位：毫米）

年代	材契（厘米/份）			相当《营造法式》材等
年代	材广×厚	份值（厘米）	契高	相当《营造法式》材等
963	22×16/15×10.9	1.47	10/6.8	四

表2 万佛殿主要建筑构件用材数据（单位：毫米）

檐柱（厘米/份）
径	平柱高	角柱高	生起
46/31	342/233	347/236	5/3

铺作（厘米/份）		前后撩檐方心长	举高	举高比%	总高
出跳总长	栌斗底至撩檐方背高
143/97	185/126	1363/927	360 /245	53	887 /604

表3 万佛殿铺作出跳数据（单位：毫米）

外檐外跳				外檐里跳		外檐扶壁栱
一跳	二跳	三跳	四跳	一跳	二跳	外檐扶壁栱
42/29	31/21	37/25	33/22	42/29	41.5/28	单栱四方

万佛殿的彩画、瓦石作未能得到深入的研究；殿内彩塑被认为是五代遗物，多有图版发表，但未见关于彩塑木骨、泥体、色彩等分项深入探讨。

1988年国务院公布镇国寺为国家级文物保护单位，1997年镇国寺与平遥古城和双林寺共同列入世界文化遗产名录。此后相关专业人士对于平遥镇国寺的研究逐渐多了起来，先后出版了《平遥县志》（1999年版）、《三晋揽胜——双林寺、镇国寺》（2002年）、《山西旅游风景名胜丛书——镇国寺》（2004年）、《中国彩塑精华珍赏丛书——平遥(镇国寺)五代》（2006年）、康熙四十六年八卷本《平遥县志》（2008年，其中附录介绍镇国寺）。

历史文献调研

令人费解的是，关于镇国寺万佛殿历史文献相对匮乏，地方志中竟然未见记载。所幸现场遗留一些碑刻与建筑题记等珍贵的文字资料。这些资料与现存相关史料对照，可约略对万佛殿之起源、沿革、匠作传承做出梳理，为更为广泛视野下的研究提供背景素材。兹摘要罗列如下。

1.1

地方志

王炳吉先生在为2008年出版的康熙四十六年八卷本《平遥县志》撰写的前言中认为平遥编修志书的年代“大概”是：

（1）金代（1115-1234年）首纂《平遥图经》；

（2）明嘉靖年间（1522-1566年）始修志书；

（3）明万历初年，以嘉靖志颇多阙略，历四十余年，至万历四十五年（1617年）杨廷谟主持编修十二卷本《平遥县志》；

（4）康熙十二年（1673年），陈以恂、梁雉翔纂修《重修平遥县志》二卷；

（5）康熙四十五年（1706年），王绶有主持编纂《重修平遥县志》八卷；

（6）光绪八年（1882年），恩端主事，成《平遥县志》十二卷；

（7）1999年，平遥县地方志编纂委员会编写了最新的《平遥县志》，由中华书局发行。

1.2

碑刻

万佛殿内现存碑刻20通，有的陈列在东西碑亭之中，有的嵌于万佛殿南墙之上，其中关于营造历史的碑刻共有5通，能够提供部分历史信息的碑刻12通。按照时代顺序分别整理其所在位置及其内容如表4，并在其后附其余各碑简要信息。

表4 万佛殿现存碑刻一览

向上滑动阅览

东碑廊

半截碑

一行：可能乎记

二行：圣运昌麒麟降而仁君霸，推兹时端方并

三行：则匪懈于尊贤容众，左辅弼进思尽忠。类八柱以擎天，高明之位定；同五岳以镇地

四行：大六帝握符，缵文继武，序祖爱遵于实录，历代罔列于

五行：幽谷。显列风尘之外，迥异天地之中。识星恢弘，宛为人杰；仪形俊迈，甚越龙驹。才当

六行：仁竦于邹衍。师资之礼既异，生知之学甚殊。耀美文昌，中山之词锋莫敌；杨芳

七行：诸王方将永赖于盘维，岂意返遗于弓剑。哀哀泣血，仰圆盖而恨夺

八行：太古之风，缮甲治兵，待静中原之难。于是兑总泽，访英贤，外委方虎之

九行：禄石辞于内举，遂授王银青光禄大夫、检校司空、右卫将军兼御史大夫、上柱国

十行：王始统领于北军，显陟将坛，恒参相府。王既当典武，仍处极言翊卫则知无不

十一行：□于匡时，敬敷王教。王情深寅亮，道切弼谐。殊勋实挎于前修，令誉弥宣于□

十二行：艺故迁三事之资。焜耀九逵，掩吕虔佩刀之贵；喧哗四海，鄙王剪分阃之荣，志抱于铁

十三行：大夫、检校太傅，进封开国子，食邑五百户，表周堪谏诤之能；门施行马，重陈骞机

十四行：鱼进户封未酬《湛露》之私，遽负《蓼莪》之痛，即以睿宗皇帝宫

十五行：景宗而践祚。克佐成王之运，善逾康叔之能。寻于天会十二祀，加检校太尉

十六行：勋，奈旷守文之位，乃扶今圣，克绍宝图，举国维以复张

十七行：都检点兼归义府都督，旌其能也。王以帝室深严夙夜之警，巡罔迨下

十八行：校太尉、彭城郡开国侯，食邑一千户。剪桐分宝，用光伯叔之荣；建社苜茅，回表藩

十九行：之□□享年二十有二

郝同村镇国寺重建东廊碑记

盖尝闻之为善最乐，福缘善庆，以是知修建禅林乃神器大典而功德无量者也。余乡镇国寺建自有汉，乃奉皇帝相公以及文武寮采，央工起建，为吾郡名胜，而东殿设像大士阿罗，当年殿宇辉然耸峙，宝象森严，延之奕禩，年深日久，风侵雨蚀，颓然圮坏，而纠首住持重新修建，按地亩摊凑布施七十余金，住持募化布施九十余金，不逾年而殿宇辉煌，宝象如故。工成之后，首事诸人向余征文，勒石以垂久远。余不禁踊跃而叹曰：修寺建塔，诚盛举也，乌可淹没不彰？于是斋戒虔兢，约略类词，将诸善士姓名刻勒碑记，以流芳后世云。

口上总理纠首郝之才；众纠首：田生文、郝秀功、郝宗圣、郝秀玉；京城经理纠首：孔奇宪、郝富盛、吴天富、米惟成、杨俊才、郝之珍、吴天明、裴亮明、阎清、杨俊福、郝之禹、裴吉仁、宋国成、梁定文、郝之先、孔清圣；

本村经理纠首：郝文强、武尔金、田生颖、郝世显、郝世奇、米惟一、郝志唐、郝世贤、高进宝、郝之宁、郝世典、郝世卿、田稷、米瑞、郝之正、郝世禄、郝世荣、郝世美、郝光宗、郝应奇、裴吉太、杨俊奇、白大功、郝世珍、韩建成、白奇章、裴吉宝、郝之显、梁定库、裴毓秀、阎重、吴德祥、裴尔仓、裴良宰

东半村住持僧人：法荣

门徒：悟成、悟明

徒孙：真好、真行、真泰

重孙：常锦

庠生郝世明谨撰郝世美书

大清乾隆十七年岁在壬申阳月谷旦立

西碑廊

重修西廊房碑记

尝闻《太极图》云：无极而太极，太极动而生阳，静而生阴，一动一静，互为其根。以是知有阳则有阴，有阴则有阳，阴阳之礼，自古昭然。本乡镇国寺西廊房地藏、阎君皆幽冥之王、地府之尊，彰善瘅恶，报应至灵，当年殿宇辉煌，金身彩焕，固为一乡之望，逮至奕禩，年深日久，未免风雨侵坏。本乡纠首住持目击心伤，内外募化，重新修建，不数日而焕然维新，灿然改观。此非一力之可成，实赖众善之乐供。目今功已告竣，理宜勒石著名，同受景福，谨将信士姓名、布施开列于碑，以垂不朽云。

郝世美谨撰书

本寺住持：曾祖师如祥，师祖智仁，师庆虎，己身祥财、祥银、祥宝，门徒普福、普然、普吉、普禄，孙原来。

乾隆四十六年岁次辛丑菊月吉旦

郝同村补修古寺记

始事匪难，终事惟难；乐成菲难，图终惟难。《诗》曰：靡不有初，鲜克有终。《书》曰：为山九仞，功亏一篑。盖图终若是之难也乎？

郝同村古寺创始于北汉，重修于前明中，惟中殿为鲁灵光，而前之山门、后之佛阁、左右之东西廊皆后人续而成之者。

然庙故多隙地而屋宇寥寥，殊非所以崇庙貌、壮观瞻也。丙辰之岁，乡之人始议补修，乃建舞榭一于山门之外，经堂一于佛阁之西，工犹未已也，会执事人有卒者，所得中外布施暨财力出入帐薄多致散失，以故不获，建石书名，补修之，事遂寝。既而乡之人相与议，谓事有始而不有成，非计也；有与开其先而无与继其后，非功也。今日之事其不可以不终，乃计产出资，于佛阁之东更建经堂，以配其西；而以其财力之余，度庙中隙地而皆属之，计东西共得屋凡六间，而后功既多于前人而补修之事始告竣矣。独是郝同仅弹丸地，又无富家巨族，力能独任丙辰之役，犹或求助于异地，自是以后，力役迭兴，凡一木一石，无不取给于本乡者而力不竭而财不匮，数年之间成此盛举，则是乡人乐善之诚与执事者用心之苦不亦深可嘉哉？余自少读书其地，今岁复过之，见其廊宇修整，光景一新，乡之父老有识余者，为余述其巅末，而乞余为记。余既喜斯寺之改观，而因以知是乡之人为可与始事也，能终事也；为可与乐成也，善图终也。略述其概，以告后人之继起者。

庚午科解元大陵苏捷卿眉仙氏沐手谨撰

大清嘉庆十八年岁次癸酉十月十六日

万佛殿南壁

咏双龙槐（略）

癸酉拔贡古梗阳季真岳峤题

龙槐行（略）

郡痒生卧楼郝元龙题

龙槐赞（略）

七言绝（略）

七言律（略）

邑庠生大有田逢年题

阖村董事人公立

大清嘉庆岁次癸酉梅月刊

镇国寺龙槐记

古陶树木之奇有二，曰柏仙，曰龙槐。胡村柏仙观，载诸邑乘。而龙槐在郝同，虽本邑人士，罕有知者，良可惜也。丙寅冬，余自闽归来，诣郝二年伯瑞府翁，话及其事，瑞府翁慨然曰：槐之托根于兹寺久矣，槐之阅历，夫游人骚客亦不知凡几矣。竟无只字表扬，与兹槐生色亦一憾事。君其援笔以纪之可乎？余负诺责久，至已巳夏，乃迟迟有以应命焉。夫树之参霄翳日，指雾披云者，如龙门之桐，泰岳之松，大都以耸直为胜，而是槐独以盘曲为胜。槐在寺中大殿前，东西两株对植，高不过寻丈，其枝委地，与其身等。根之诘曲而蟠踞于地上者，亦与其身等。仰而望之，一枝百折，互相纠结，如循环之无端，如檐牙之斗角。老干虬纹，霜皮石裂，此则槐之大概也。若夫鼠耳齐圆，金花并发，披枝而内视，碧叶四垂囷囷焉。似蟠龙之奋，苍髯绕荫，而外观密条双绾，森森然似卧龙之蜷翠鬣。每当轻颸乍到，叶飒花飞，真有如古诗所谓风动槐龙舞者矣。至若秋冬气凛，霜雪交侵，柔枝蠖屈，劲枝爪伸，苍莽骈叠，端倪莫寻。夜月如水，宛映贝阙之双白龙。又可矫然拔俗也。吾闻槐为虚星之精，得此两槐，洵足称列宿之仙灵，作文坛之佳话矣。而乃地异通衢，庙邻僻壤，不克传播于大方之耳目。与柏机互相辉映，斯吾之为槐恨者也。然槐之有两，则又若幽侣相伴，数百年来，亦颇不寂，使非寄迹招扌，与老衲共数晨夕焉。知不早斧于樵夫之手，又孰为持护其枝干，以令其偃仰，至今而久居此寺中哉。始建于北汉天会七年，时宋太祖建隆三年也。重修于金天德三年，时宋高宗绍兴二十一年也。相传有此寺即有此槐，盖八百馀年物也。吾今志之，非特彰龙槐之名，抑以见村众人之好古，有不愧雅人深致者焉，是为记。

赐进士出身文林郎历任云南宣良、福建福鼎县知县梗阳岳廷元撰

大清嘉庆岁次癸酉梅月谨刊

重修镇国寺第二碑

余少有好古之癖，凡远近所有古迹，遇之辄徘徊不忍去。总角时从余师茹可先生读书于平邑之郝同村镇国寺，寺中隙地固多而屋宇寥寥，中有中殿，剥落更甚，然其规制奇古，绝不类近世所为。或曰寺创于北汉孝和帝天会七年，殿固原建时所营；或曰元明时所重修者，惜无碑碣可考，然大约数百年物也。余时与朋辈游览其中，为之惋惜者久之。

辛未岁，里之执事者以状来乞余为记，姑知庙中隙地皆已部署为屋，而无一语及所谓中殿者，既为之记以去，而心尝缺。然今岁丙子复得执事者之状，据云中殿之修所费不赀，自辛未岁始与乡人约令，其计地均派每夏及秋亩出麦或粟各一升；又按户授以疏引，使家自为募，凡得叁千或百余金而后举事。先是殿之墙宇虽圮而基址如故，遂因其旧而葺之，勤垣墉，涂墍茨，凡栋梁之摧折者皆易焉。而复令设色之工施以藻绘，事既成而犹有余力，乃分葺其东西廊，而于中殿之前新建左右碑亭各一。又屋庙西隙地得社房十三间，庙之东偏旧有元坛一所，亦续而重修之。盖事虽半出于因，而功则几同于创。自丙辰岁始，凡经营二十余载，而后所谓“镇国寺”者至此而焕然一新。

呜呼！是乡之人可谓乐善不倦者矣。虽然，余于是役不喜其功之成，而喜古迹不湮没于今也。夫吾人生居輓近，见古人一器一物必什袭而藏之，惧其久而敝也，必为之刮磨而修整之，而况巍峨如斯寺者乎？吾不知是乡之执事者仅乐善之诚欤？抑由好古者笃欤？未可以臆度也。然使于二者择一而处焉，亦余之所乐为记者矣，而况斯役之成，又与余好古之素志有合也哉？故详述之，以垂诸后之乐善如乡人而好古如余者得览焉。

庚午科解元大陵苏捷卿沐手谨撰

丙寅岁贡元邑人许世卿沐手谨书

经理纠首：郝清植、裴天成、郝光绅、田增檍、郝光兴、郝秉仁、梁永广、阎名扬、高攀凤、裴大命、吴文盛、杨清梁、郝秉盛、武明章、白世兴、郝瀛洲、裴正德。

嘉庆贰拾壹年岁次柔兆困敦菊月中澣之吉

半截碑记

半截碑者，不知何人所书也。嘉庆年间，庙工告竣，会立碑之际，欲作碑座，形象已成。余祖增檍公见而止之曰：“此碑书法甚好，不可毁也。存之以为学书者临摹。”嗣后，爱而拓之者甚伙，但上下文义不全，观其大势，是当日封王于此，且天会十二祀，年号殆亦八百余年物也。惜碑太厚，未克嵌壁，今筑小台安置其上，于是乎记。碑亭中间所裱，明状元刘理顺大草墨迹剥落太甚，将诗勒石以志不忘：“林间挂葛巾，树里峰阴转。山外首频昂，白云无近远。”

恩贡生田耕蓝谨撰并书

大清光绪拾年岁次甲申荷月上澣吉立

借寺屋作书馆偶题

郝大老夫子，鉴，字茹可。乾隆辛卯科举人，设馆于此寺。题诗一首：

慧业文人景谢郎，禅堂今作读书堂。

我来不是逃名位，要借佛家一瓣香。

道光年间有优人观龙槐题诗而去，今观诗意，殆诗人隐于优者与：

黛色经天映落晖，一枝百折世间稀。

幽禽亦识龙槐意，独占高稍不忍飞。

偕砚友郝君步宫观双龙槐恩贡生田耕蓝

殿前笑语共徘徊，枝干离奇仰古槐；

何日风云时际会，神龙逃下一双来。

双影婆娑佛殿前，妙方插接忆当年；

即今每遇风雷起，鳞爪如生欲上天。

大清光绪十年岁次甲申署月上浣吉立

西碑廊

龙槐荣枯记

龙槐之由来，前碑已详言之，兹不再叙。而今数十年来或枯或荣，则有不可不志者。东边一株于道光十二、三年，从树身生出一枝，与常槐同，初以为小，曾不在意。十数年后，枝大于身，将一身之精神气脉，皆为此枝所拔。而全树之枝叶枯槁殆尽。见者忧之，不敢擅动。同治年间，郝翰藩先生，有胆有识，为文以祭，命梓人斧以斯之，人心大快，此枝一除而全树之枝叶渐见，发生迄今，大有可观矣。至于西边一株，道光初年即见皮有破裂，心亦空虚，而枝叶亦不畅茂。正如昔人所谓，此树婆娑生意尽矣。至咸丰间，小枝尽枯，止存老干，槎枒数枝而已。忽从树根发出数株，亦与常槐等。今已长大成树矣。昔有一差人言，此树是插接所成。当时以为贱役小厮，何足为信。今想东边所生之枝，与西边所发之树，且细视树身有插接痕，上下之树皮不同，枝叶不同。然后知差人之所言非妄也。

例授修职郎侯铨教谕里人田耕蓝谨撰书丹

大清光绪拾玖年岁次癸巳中秋月下浣吉立

社仓丰备仓记

光绪二年秋九月，明府汪公缘事来村，茶话之间，公言欲为各村创立社仓，为备荒之上策。不料秋后收成歉薄，三年更遭大祲，赈务浩繁极矣，奚遑为社仓计哉。五年夏五月，公升任阳曲，余约邻村组饯于洪善驿，公犹以社仓未立为憾。六年锡公莅任，奉上宪发来钱，按官马均分。令各村量买仓谷，名为社仓。秋后又令各村每亩地凑谷一升，名为丰备仓。公轻骑减从，下乡新查，又令余笃代查东北乡各村仓谷，然后知此事仍是汪公暗中调度也。呜呼，公在任时，在功德于我邑者，人知之。公离任后有功德于我邑者，人皆不知也。此余所以再四思维而不得不记也。嗣后，愈积愈多，派仓长二人经管，纠首、乡保、住持一并看守。每岁三、六、九月起差之日，公同查阅。倘有房屋渗漏，即为葺补；仓谷霉变，即为晒晾。岁以为常，不可废弛，庶不负上宪及二公思患预防、谆谆告诫之良法美意也，是为记。

汪公名守正，浙江钱塘诸生，现任直隶宣化府知府。

锡公名良，汉军旗人进士，现任平阳府知府。

例授修职郎吏部就职侯铨教谕恩进士田耕蓝撰并书

仓长：田耕蓝郝步宫

纠首：裴春云白全龙康步霄裴永义郝金雕李联琛武效唐郝鸣鹿郝文信阎炳南武廷瑶

乡保：郝发兆阎九德

住持：眼广

大清光绪二十年岁次甲午季春中浣之吉日公立

东碑廊

补修镇国寺并九间庙碑记

天下事岂有难为哉？知其难而畏首畏尾，退缩不前，则难诚难矣；知其难而无怠无荒，踊跃从事，则难非难矣。

我村旧有镇国寺一所，创自北汉天会七年，元明以来代有建修，自嘉庆二十年补修，迄今九十余年矣。又有大寺西九间庙，道光初年补修，迄今八十余年矣。合而计之，历年既多屋宇摧残，屡议兴修而工程浩大，不敢轻举。有白君昌龙先生，会集公所，每欲举事，自云性情暴躁，难以终事，众皆曰：不然，事以渐进而成功，以陆续而积。

自光绪二十一年执事者慨然有志兴修，公议从地亩起派以及花户人名布施兼四外募化，于是鸠工庇材，土木交作，诸处仍旧葺补。惟有村中大街南北门三灵侯福财神庙，咸丰初年建修，嗣后皆以为财神过路，财不能聚，光绪二十四年五月卜吉分移于大寺东西碑亭之北，较前得所。

更可异者，他处木质多年朽腐，惟中殿木质几近千年，完好如故。观其庙貌奇古，欂栌节棁结构非常，询之能工巧匠，皆不知从何而起，从何而止，相传鲁班所造，非人力所能为也。遐思此寺创始，疑是一大都会，惜无可考。惟有半截碑，上下文义不全，阅其大略，是当日封王于此。呜呼，庙貌依然，当日之风景不可复观。

虽然经营数载，土木之工虽具，绘画之事未完，本欲次第兴作，告厥成功，无如饥馑薦臻，起派维艰，为之停工者数年。今幸而岁值大有，四外募化亦源源而来，因而续成前功，缺者补之，旧者新之，丹者金碧，东西掩映，焕然改观，所有前后一应工料之费，俱详于碑阴之末。由是观之，功以缓成，多历年所，而诸君经营筹画，无敢怠荒，不以为难，可谓勤且劳矣。余喜其功已告竣，援笔而为之记，泐诸贤（石民）以告后之继起者，勿以难为而弗为焉。

例授修职郎候铨教谕壬申乡贡里人田耕蓝沐手撰

例授修职郎候铨儒学本邑庠生里人李观远篆额并书

经理纠首：都司衙阎炳南、同知衙白全龙、同知衙郝金雕、从九康步霄、武效唐、武廷瑶、裴步云、郝时来、从九李卿芳、王植芳、王光明、从九郝鸣鹿

督工：郝春青、阎炳琅

大清光绪叁拾年岁次阏蓬执徐中和月下浣之吉立

因缘簿失序记（碑阴）

庠生李观远谨撰书

书匠：郝子英、郝有玉、张长富、邢增福、许凌魁、温登科、温子恭、姜福昌，襄垣村和顺石厂

木匠：梁统宗、裴有成、郝玉明

泥匠：杨真日、王立孝、裴有起、田纪则、裴振玉、杨树芝

铁匠：李文秀

漆匠：元泰涌、源通海

细木匠：崔广华

住持：眼广、友尚、韩永隆

1.3

建筑题记

万佛殿内建筑题记共有8处，分布在屋架和墙面之上。按照时代顺序分别整理其所在位置及其内容如表5。

表5 万佛殿现存题记一览

向上滑动阅览

脊槫底

维大汉天会七年岁次癸亥叁月建造

东四椽栿底

奉为皇帝相公及文武宷寮建造佛殿壹所愿法界生灵同登觉道

西四椽栿底

郝同村院主僧 □诠业维摩经僧继鸾继钦

讲百法论上生经僧继麟

业上生经继圆继□ 继晖

业上生经继伦继杲沙弥佛有福兴

村众梁章高实郝德郭崇梁斌兰能王荣宋豊……

兰岳郝茂宋武郝贵郭嗣宋实杜斌王进……

杜莒宋章杜威刘晖张珙张钦郝成张莒……

郝宝梁崧张荣郭豊郝遇梁琪阎义邓崇……

客户任立高太温珎毕晖魏珣梁温王諲胡蕴……

杨德宋崇阎晖郭福吕珣弓友赵茂李遇……

李建张德张进周铎成美孟岩武珣孙德……

成萼张威郭温郭思王威王进武荣阎茂……

木作都料李绍琮弟绍珎博士崔延美弟诚训

赤白都料李彦宗弟彦柔彦赟

结瓦都料郝绍琼弟绍諲铁匠李谏绍丕彦宗

打瓦都料武彦玫吴敬超石匠李进

前上平槫下之上襻间底附板

大金天德三年岁次辛未七月补修

前下平槫下之襻间底附板

大明嘉靖十九年岁次庚子二月补修京城寺改为镇国寺

倒座观音背光上附板

金粧观音菩萨圣像功德人弟子郝之正施银叁两（查郝之正之名见于乾隆十七年郝同村镇国寺重建东廊碑记：“……京城经理纠首：……米惟成……郝之珍郝之禹、裴吉仁……郝之先……；本村经理纠首：……米惟一……郝之宁……郝之正……裴吉太……裴吉宝、郝之显……”）

前上平槫下之下襻间底附板

大清嘉庆二十年岁次乙亥三月重修

脊槫下四椽栿上所架附板

扶中梁功德主高祖父郝文华（高祖）母许氏曾祖父世光（曾祖）母张氏祖父士功（祖）母高氏父全德母秦氏己身现云元乘龙妻申氏杨氏张侯秦氏田氏男天申（妻张氏）佑（妻任氏）助施银柒拾两大清嘉庆二十菊月谨誌

1.4

历史线索综述

“四有档案”记载，1949年以来，一直未有规模维修万佛殿的工程，直至2009年，修缮万佛殿屋面，捉节夹陇，勾抿灰缝。

根据碑记、题记、史志等所有已知历史维修记录，已经可以初步梳理出万佛殿经历的一些重大工程。在此基础上，精细测绘所发现的木作、瓦石作、彩画作修缮痕迹可以对这些文字记录进行证实或者补充。兹按照时代先后次序罗列文字史料如下。

（1）碑文中提到“睿宗皇帝”，系北汉第二代皇帝刘承钧之庙号。刘承钧卒于天会十二年（968年）。说明此碑成于天会十二年之后。

（2）殿内屋架题记分别说明大殿及其附属文物至少经历了以下修缮工程：金天德三年、明嘉靖十九年、清乾隆十七年前后、清嘉庆二十年。

实测方案

从当前保存状况来看，万佛殿的木结构并非完全暴露可测。万佛殿仅用立柱一周，均掩藏在后期砌筑的墙体之内，且墙体下脚未见暴露柱础，立柱上端暴露54厘米至62厘米不等，前后外檐装修皆结合墙（图2、图3）。在这种情况下，木结构的测绘重点为柱头以上部位，尺度设计、保存状况无法涵盖柱身及以下部位。重要的是，柱头以上的梁架大木结构最复杂、形变情况最复杂、材料劣化最复杂；不仅需要采集形变较小部分的数据——如同常规“法式测绘”，更需要在形变显著的部位也小心选择相对可靠的度量，以增加数据采样数量，以增加逆向分析可靠性。

图2 万佛殿外景

图3 万佛殿鸟瞰图

3.1

柱头平面

本测绘方案只能强调测量露明的柱头尺寸。柱脚测量采取手工与三维激光扫描结合的方法；柱头测量主要结合全站仪和三维激光扫描进行数据采集。

由于全站仪和三维激光扫描仪等设备的主要工作平面是地面，工作高度在1米至2米之间，难以实现俯视扫描而获得直接的柱头平面数据。本测绘中采用的便利方法是用柱头附近斗栱构件（头跳华栱）的底面楞线、中线的关系距离替代直接数据，同时记录柱头部位额、枋的拔榫或挤压现象，再通过多位置采集数据的方式降低误差，最终确保数据精度达到两次测量读数较差不超过（3 + 0.001L）mm之规定（L为被测长度）；同时各分段测量值之和与一次测量值之和之差不超过 0.004∑Li（Li为各分段测量值）。

在各内外立面开间数据提取过程中，工作方针是尽力提高单站内数据的覆盖率，避免不必要的多站拼合，从而实现提高数据精度的目的。

3.2

梁架

构件之间相对关系数据利用三维激光扫描仪量取；梁架中各槫、栿、串、额、柱等构件的尺寸采用手工测量取得。梁架部分测量原理、数据精度标准与平面部分相同。

在研究阶段梁架构件相对距离的测量也适合采用三维激光扫描技术、单站提取数据的方案。所不同的是梁架构件互相遮挡的现象比较严重，无法实现数据的绝对完整。

再有，本测绘还强调，须在基础测量之外特别注意到结构的构造逻辑、交接关系和细节做法，强调从营造本身的角度理解设计者的思路。

3.3

斗栱

斗栱测量不是针对一朵所谓的“典型构件”进行穷尽的测量精确化，而是在更大程度上把握斗栱空间姿态和形变特点，在每朵斗栱中寻求最接近原始设计的特征数据，并进而在多朵斗栱中展开广泛测量。

斗栱实测长期以来以半厘米为精度标准。考虑到长期以来传统测量方法对斗栱空间姿态把握困难，在各个单站内利用三维激光扫描与手工测量结合的方法可以将斗栱量取和分析精度提高到毫米级。

由于三维激光扫描单站之中对斗栱可见构件的相对尺寸的测量——如出跳距离、足材高等——具有极大优势，而对于一些单体构件在可见、不可见表面之间的距离的测量——如构件厚度、高度等——须经过拼站处理，反而降低了数据精度，不如手工测量。实测中应当采用扫描与手工测量相结合的方法。针对斗栱数据的采集方案简述如下。

（1）材广、材厚：手工多次测量形成数据表，筛除特异值，确定取值区间，其中材厚数据以手工测量最妥，在测量条件允许的情况下也应补充手工测量材广；

（2）每跳出跳高度、水平出：

参考水平标高、构架轴线，调整构件姿态；
尽可能合理地提取出跳构件、横向拉扯栱外皮之间的相应距离；
在出跳构件两侧分别测量，消除构件组扭转形变的因素；
以手工实测的栱、昂厚度校核出跳高度、水平出。

斗栱中各横向栱、大小斗等构件的规格尺寸应当采用手工测量方案。

3.4

测量仪器站点分布

本次测绘使用的全站仪型号为Sokia530R；三维激光扫描仪为Bitwyse（现属美国Surphaser公司）之3Dguru设备，工作原理为相位激光测量，测程范围为0.3-36.7米。

全站仪、三维激光扫描仪，仪器测量以地面为主要工作面，站点分布力求覆盖测绘对象之木结构所有可见部分，但是由于角落位置构件相互遮挡，且无法架设机站等因素，未能获得扫描数据或点测量数据（图4）。

图4 万佛殿三维激光扫描仪、全站仪布站图

由于现场脚手架、工作时间等因素的限制，2010年测绘中手工实测的覆盖面并未达到大殿所有露明部位，砌筑与墙体内部和交接与构件内部的隐蔽部位未开展精细测量工作。立柱层、斗栱、梁架层基本得到完全覆盖；隐角梁、生头木等难以揭露部位仅开展典型构件测量。

平面丈尺实测与分析

4.1

柱头间距

万佛殿用檐柱一周12根，柱头露明。然而由于柱头与阑额、栌斗相交，无法直接确定柱心，也难以准确拟合柱心位置。在本次实际测量过程中，采取间接测量方法——以头跳华栱底面楞线的关系为准测量柱头铺作中心的距离，同时记录柱头部位阑额的拔榫或挤压现象。为了进一步消除华栱厚度不同等因素带来的误差，在测量其底面楞线间距时分别测量左右两侧数据，用全站仪配合手工测量得到数据表。

就此，提取并计算柱头间距如表6、图5（系列1代表面阔明间，系列2代表进深明间，系列3代表面阔和进深次间），并在表7中进行分布情况分析。

表6 万佛殿柱头间距实测数据归纳表（单位：毫米）

	面阔西次间	面阔明间	面阔东次间	进深南次间	进深明间	进深北次间
南立面1	3503	4477	3511	–	–	–
东立面1	–	–	–	3496	3662	3493
北立面1	3522	4485	3506	–	–	–
西立面1	–	–	–	3491	3690	3511
南立面2	3482	4480	3516	–	–	–
东立面2	–	–	–	3482	3669	3508
北立面2	3525	4483	3523	–	–	–
西立面2	–	–	–	3508	3686	3514

考察结构对称和转角关系，可以认为：面阔东西次间、进深南北次间之间存在相等的关系。

图5 万佛殿柱头间距实测数据分布情况

表7 万佛殿柱头间距实测数据统计分析（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
面阔明间	4481.3	4477	4485	12.3	4
进深明间	3676.8	3662	3690	179.6	4
面阔和进深次间	3505.7	3482	3525	185.4	12

按照“间广进深半尺假说”，以均值为准推算柱头间距用尺如表8所示。

表8 万佛殿柱头间距用尺推算（单位：毫米/尺）

测量对象与推算	面阔明间	进深明间	面阔和进深次间
实测数据	4481.3	3676.8	3505.7
估算用尺	14.5	12	11.5
倒推营造尺长	309.05	306.40	304.84
权重（数据量）	4	4	12
推算结论	1营造尺=306毫米
实测折合营造尺	14.64	12.02	11.46
吻合程度	99.00%	99.87%	99.62%

需要说明的是，除306毫米用尺之外，还可能存在诸如294毫米之类的营造尺长的可能性。此处选取306毫米的原因有二：

（1）具有最高的吻合程度——全面达到99.00%以上；

（2）此推算与外檐铺作材广厚数据吻合极佳（参见下文）。

4.2

柱径

虽然万佛殿12根立柱件用材较为规整，但是由于阑额、栌斗等相交构件的遮挡，柱头部位又有卷杀，柱径无法直接量取。在现场量取并予以估算调整的基础上，降低测量精度要求，得到柱径实测值46厘米。此数值与陈明达先生整理公布的柱径数值相同。

进一步参照上文推算所得营造尺长306毫米，柱径折合15.03寸，取整为15寸，吻合程度达到99.78%。参考下文可知柱径用2材，与《营造法式》所规定的“凡用柱之制：若殿阁即径两材两栔至三材；若厅堂柱即径两材一栔；余屋即径一材一栔至两材……”相比，用材偏小。

4.3

角柱生起

由于万佛殿柱头长期受到集中荷载，可能存在诸如柱身倾斜和受压形变不均匀等现象，因此实测数据不能准确反映角柱生起的原始设计值。现将实测结果汇总得到表9。

表9 万佛殿柱头生起推算分析（单位：毫米）

	西南角柱生起	西-东平柱	东南角柱生起
西南测站	9	-53	54
东南测站	未及	未及	51
	西北角柱生起	西-东平柱	东北角柱生起
西北测站	8	19	9
东北测站	10	12	10
	东南角柱生起	南-北平柱	东北角柱生起
东南测站	68	-7	未及
东北测站	未及	未及	-18
	西南角柱生起	南-北平柱	西北角柱生起
西南测站	53	2	64
西北测站	未及	未及	67

考察表中畸变数据，能够看出西立面生起规整，而西南、西北、东北角柱低于东南角柱，在无法测量柱脚的情况下，只能大胆推测西立面立柱有向东倾斜的趋势，而东北角柱有向南倾斜的趋势。于是，从上表数据中取51至68毫米的生起值为有效值，剔除其余测量值，生起均值为59.5毫米。参照306毫米营造尺，初步推算万佛殿角柱生起2寸，吻合程度为97.22%。此推算与《营造法式》中“至角则虽间数生起角柱……三间生高二寸”的记载相符。

4.4

总结

初步分析可知万佛殿平面丈尺设计方法如下：

（1）面阔明间1丈4尺5寸，吻合程度达到99.00%；

（2）进深明间1丈2尺，吻合程度达到99.87%；

（3）四面次间开间均为1丈1尺5寸，吻合程度达到99.62%；选择半尺作为与外檐铺作及其里转部分尺度设计相关的次间开间，具有更深层的设计伏笔，参见下文；

（4）柱径1尺5寸；

（5）角柱生起2寸。

外檐斗栱实测与分析

镇国寺大殿斗栱布置在外檐、内檐、天花装修等处。外檐斗栱面阔方向当心间用补间铺作两朵，次间用补间铺作一朵；进深方向，前、中二进用补间铺作两朵，后进用补间铺作一朵；内檐斗栱随外檐斗栱布局规律安设。其中外檐斗栱有9种不同形式，分别为前檐柱头、补间、转角铺作，后檐柱头、补间、转角铺作，山面柱头、东山面补间铺作，西山面补间铺作等；另使用内檐斗栱有7种，即前内柱柱头铺作，前内柱柱中铺作，后内柱柱头铺作，前内柱内额间斗栱，后内柱内额间斗栱，前三椽栿上补间铺作，乳栿上补间铺作，平梁梁端斗栱。

外檐斗栱基础数据的采集是揭示大木结构设计规律的第一步。鉴于下昂坡度问题的复杂性，将结合出跳和跳高的基础尺度设计在下文中展开讨论。

5.1

材广厚

（1）华栱广

外檐铺作四立面正身部分各显7朵，每朵采集一二跳华栱各一，实测数据56组，分布情况如图6。其中取值分布在205毫米-227毫米之间的为各单材华栱，施用于补间铺作和转角铺作正身部位；取值分布在300毫米以上的为各足材栱，施用于柱头铺作和转角铺作的斜出部位。

图6 万佛殿外檐铺作华栱广实测数据分布情况

万佛殿外檐铺作单材、足材华栱广数据统计结果见表10。

表10 万佛殿外檐铺作华栱广实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
单材华栱广	214.1	205	227	30.15	40
足材华栱广	316.4	299	329	50.91	20 （补转角4组）

（2）华栱厚

实测数据60组，分布情况如图7。

图7 万佛殿外檐铺作华栱厚实测数据分布情况

万佛殿外檐铺作华栱广数据统计结果见表11。

表11 万佛殿外檐铺作华栱厚实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
华栱厚	155.7	150	166	11.83	60

对照前文推算出的营造尺长306毫米，假设华栱厚度为10分°，考虑到华栱长期集中受压，倒推得1分°=0.5寸=15.3毫米，吻合程度为98.24%。综合考察华栱广厚情况可有表12。

表12 万佛殿外檐铺作华栱广厚材份推算分析（单位：毫米）

测量对象与推算	足材华栱	单材华栱	华栱厚
实测值	316.4	214.1	155.7
折合分°	20.68	13.99	10.18
取整分°	21	14	10
受力情况说明	集中受压	集中受压	集中受压
变形情况说明	存在受压减小趋势	存在受压减小趋势	存在受压增加趋势
吻合程度	98.47%	99.95%	98.24%

（3）昂广

头昂、二昂广实际是相同的，考虑到三维激光扫描点云数据更为有效，而进一步考虑到提取过程中的实际效果，头昂测量连带栔一并计算最为实际和方便。因此，实测得头昂、二昂各16组及头昂单材部分16组，分别计算，分布情况如图8、图9。

图8 万佛殿外檐铺作头昂单材及二昂广实测数据分布情况

图9 万佛殿外檐铺作头昂足材部分实测数据分布情况

万佛殿外檐铺作昂广数据统计结果见表13。

表13 万佛殿外檐铺作下昂广实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
头昂广	278.4	269	287	18.66	16
二昂广及头昂单材部分	187.0	177	198	21.8	32

可见，万佛殿所用下昂之广并非单材，亦非足材；通过观察三维激光扫描点云特征，还可以判断二下昂组装完毕后在垂直地面方向上高度约合2材1栔，使得上一昂上皮恰过二跳外皮与耍头下皮的交会处。此构造关系将在后文中讨论。

图10 万佛殿外檐铺作下昂与栱楞关系示意图（东南头-L.dwg）

（4）昂厚

头昂、二昂广相同。采用手工实测得数据34组。分布情况如图11。

图11 万佛殿外檐铺作昂厚实测数据分布情况

万佛殿外檐铺作昂厚数据统计结果见表14。

表14 万佛殿外檐铺作昂厚实测数据

统计结果与推算分析（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
昂厚	154.0	141	165	27.30	16
折合分°	10.07
取整分°	10
受力情况说明	受压受弯
变形情况说明	难以判断
吻合程度	99.35%

（5）栱广

采用手工实测得瓜子栱广数据44组。分布情况如图12。

图12 万佛殿外檐铺作瓜子栱广实测数据分布情况

万佛殿外檐铺作瓜子栱广数据统计结果见表15。

表15 万佛殿外檐铺作瓜子栱广实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
瓜子栱广	214.7	201	227	40.26	44

采用手工实测得慢栱广数据44组。分布情况如图13。

图13 万佛殿外檐铺作慢栱广实测数据分布情况

万佛殿外檐铺作慢栱广数据统计结果见表16。

表16 万佛殿外檐铺作慢栱广实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
慢栱广	218.9	209	237	36.43	44

采用手工实测得令栱广数据28组。分布情况如图14。

图14 万佛殿外檐铺作令栱广实测数据分布情况

万佛殿外檐铺作慢栱广数据统计结果见表17。

表17 万佛殿外檐铺作令栱广实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
令栱广	217.4	208	228	26.62	28

综合考察瓜子栱、令栱和慢栱之广，得到表18。

表18 万佛殿外檐铺作栱广推算分析（单位：毫米）

测量对象与推算	瓜子栱	令栱	慢栱
均值	214.7	217.4	218.9
折合分°	14.03	14.21	14.31
取整分°	14	14	14
受力情况说明	受压受弯	受压受弯	受压受弯
变形情况说明	难以判断	难以判断	难以判断
吻合程度	99.77%	98.51%	97.81%

（6）栱厚

采用手工实测得瓜子栱厚数据16组。分布情况如图15。

图15 万佛殿外檐铺作瓜子栱厚实测数据分布情况

万佛殿外檐铺作瓜子栱厚数据统计结果见表19。

表19 万佛殿外檐铺作瓜子栱厚实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
瓜子栱厚	156.5	150	162	8.133	16

采用手工实测得令栱厚数据28组。分布情况如图16。

图16 万佛殿外檐铺作令栱厚实测数据分布情况

万佛殿外檐铺作令栱厚数据统计结果见表20。

表20 万佛殿外檐铺作令栱厚实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
令栱厚	155.6	150	165	15.07	28

采用手工实测得慢栱厚数据16组。分布情况如图17。

图17 万佛殿外檐铺作慢栱厚实测数据分布情况

万佛殿外檐铺作慢栱厚数据统计结果见表21。

表21 万佛殿外檐铺作慢栱厚实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
慢栱厚	156.9	151	162	8.196	16

参照综合考察瓜子栱、令栱和慢栱之厚，得到表22。

表22 万佛殿外檐铺作栱厚推算分析（单位：毫米）

测量对象与推算	瓜子栱	令栱	慢栱
均值	156.5	155.6	156.9
折合分°	10.23	10.17	10.25
取整分°	10	10	10
受力情况说明	受压受弯	受压受弯	受压受弯
变形情况说明	难以判断	难以判断	难以判断
吻合程度	97.71%	98.30%	97.45%

（7）小结

通过以上分组数据统计，首先可以看出一些构件尺度相同的现象，与《营造法式》中的记载和普遍施工方式基本吻合。这些现象可以用以下等式表达：

①华栱单材厚=昂厚=栱厚，考察其均值，则∈（154.0，156.9），参考前文推算营造尺长306毫米，考虑到形变特点和原因，可以认为其厚10分°，每分°半寸；

②华栱单材广=栱广≠昂广，考察前二者均值，则∈（214.1，218.9），参考前文推算营造尺长306毫米，考虑到形变特点和原因，可以认为其广14分°；

③二下昂之广需要结合斜度设计和局部交接关系在下文中讨论；

④华栱足材广应结合斗栱结构尺度中的足材实测一并考察。

5.2

足材高、外跳出跳

通过三维激光扫描和在ACAD中提取数据（图18）得到万佛殿第一二跳总出跳、第三四总出跳（第3、第4小跳合计）尺度。

这组数据与常规的构件本体数据不同，为构件间的关系尺度。如果说构件本体尺度往往因匠人节约木材、便捷施工、历史更换等因素随宜调整的话，构件关系尺度直接影响构造间是否能够良好吻合的关键问题，即便后期修缮也必须注意到榫卯相合、对应交圈，因此可以更加直接地反映原始设计；如果说构件本体数据离散程度高、推算构件本体尺度的原始设计能够达到97%以上的吻合程度便相当不容易，根据笔者的研究经验，在构件关系尺度测量与推算中吻合程度往往可以达到99%以上。

图18 万佛殿斗栱三维激光扫描数据提取方法示意图（东北头-L.dwg）

（1）足材广

在三维激光扫描斗栱数据中，提取足材广4组每组中数据22-46份不等，分布情况如图19，图中系列1至系列4分别代表在不同铺作层上提取的足材1至足材4的高度值。

图19 万佛殿外檐铺作足材广实测数据分布情况

万佛殿外檐铺作三维激光扫描足材广数据统计结果见表23。

表23 万佛殿外檐铺作三维激光扫描

足材广实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
足材广1	319.9	309	334	39.778	46
足材广2	319.2	305	332	37.747	42
足材广3	321.6	308	330	34.909	22
足材广4	316.3	305	328	35.846	22

（2）第一二跳总出跳

在三维激光扫描斗栱数据中，提取第一二总出跳数据46组，分布情况如图20。

图20 万佛殿外檐铺作第一二总出跳数据实测数据分布情况

万佛殿外檐铺作三维激光扫描第一二总出跳数据实测数据统计结果见表24。

表24 万佛殿外檐铺作三维激光扫描第一二总出跳

数据实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
第一二总出跳	732.4	704	755	115.61	46

（3）第三四跳总出跳

在三维激光扫描斗栱数据中，提取第三四总出跳数据22组，分布情况如图21。

图21 万佛殿外檐铺作第三四总出跳数据实测数据分布情况

万佛殿外檐铺作三维激光扫描第三四总出跳数据实测数据统计结果见表25。

表25 万佛殿外檐铺作三维激光扫描第三四总出跳

数据实测数据统计结果（单位：毫米）

测量对象	均值	最小值	最大值	方差	数据量
第三四总出跳	719.5	694	753	245.88	22

（4）小结

将斗栱结构尺寸汇总，可以借以推算其间的比例关系，考察是否存在一个明确的材份制度。如表26。另，结合上文得出的数据推算，营造尺长306毫米，材厚约合0.5寸，合153毫米，吻合系数99.35%，一并归入以下推算分析表。

表26 万佛殿外檐铺作材份制度推算

	材厚	单材广	足材广	一大跳出	二大跳出
均值取值	154.0-156.9	214.1-218.9	316.3-319.9	732.4	719.5
木材形变趋势	增大	不详	减小	不详	不详
取值调整	154	218.9	319.9	732.4	719.5
若1分°=0.5尺 1分°=153毫米	10.07	14.31	20.91	47.87	47.03
取整分°	10	14	21	48	47
吻合程度	99.35%	97. 81%	99.56%	99.73%	99.94%

推算显示，如果结合平面设计中营造尺的运用，则斗栱结构尺度设计具有非常明显的趋势：

①单材广并不遵循《营造法式》规定的15分°，而更倾向于14分°；

②斗栱可以材厚为基准分为10分°，每分°0.5寸；

③第一二总出跳出48分°；

④第三四总出跳平出47分°，考察第二根下昂上皮过耍头上皮与第二跳慢栱上皮的交点，因此第三四总出跳决定下昂斜度，下昂斜度设计的基准三角形均为平出47分°，抬高21分°；

⑤自栌斗底至撩风槫底的铺作总高为106分°，至撩风槫背须再加槫高14分°，合计120分°；

⑥外檐铺作里转部分尺度与外转部分略有出入，因其不影响其他结构尺度，仅于测绘图中表现，在此不赘述。

5.3

外檐铺作实测总结

（1）交接关系

总结本节所有斗栱数据及推算结果，是得到斗栱理想模型的基础。还有一个细节问题需要解决——倾斜的下昂上下皮与正交体系的交接关系。简单讲，昂下皮与交互斗口的交接处不用华头子，头下昂自承跳斗口外楞出；上层下昂上皮恰过二跳外皮与耍头下皮的交会处。利用三维激光扫描点云影像，观察现状几个关键点A、B、C（图22），分别以吻合、略高、略低、高、低五个指标描述下昂上/下斜面与正交体系的交接关系，归纳成表27。

图22 万佛殿下昂部位交接关系参考点示意图

表27 万佛殿外檐铺作下昂关键点交接关系归纳

铺作位置	点A	点B	点C
南东角-R	略低	吻合	吻合
南东头-R	吻合	吻合	略高
南东头-L	吻合	吻合	略高
南西头-R	吻合	吻合	吻合
南西头-L	吻合	吻合	吻合
南西角-L	吻合	吻合	吻合
北东角-L	低	吻合	吻合
北东头-R	吻合	略低	略高
北东头-L	吻合	吻合	略高
北西头-R	吻合	吻合	吻合
北西头-L	略低	吻合	吻合
北西角-R	略低	吻合	吻合
东南角-L	略低	略低	略高
东南头-R	吻合	吻合	未及
东南头-L	吻合	吻合	吻合
东北头-R	吻合	吻合	吻合
东北头-L	吻合	吻合	未及
东北角-R	吻合	未及	未及
西南角-R	略低	吻合	未及
西南头-R	吻合	吻合	吻合
西南头-L	略低	吻合	吻合
西北头-R	吻合	吻合	吻合
西北头-L	吻合	吻合	吻合
西北角-L	吻合	未及	未及
统计	吻合17 略低6 低1	吻合20 略低2 未及2	吻合14 略高5 未及5

表27中A点略低处为集中受压造成；B点略低处同样如此；C点略高，与B点同处第二根下昂上皮，位于B点之后，构件前端下沉则C点相应抬高。

在以往的研究中，以五台山佛光寺东大殿为代表的北方唐辽七铺作下昂造第四跳令栱均与里跳归平（图23）。

我们知道，在已经开展过较深入讨论的三个手法类似的实例中，采用的分°值均与营造尺长存在简明的比例关系——佛光寺东大殿每分°0.7寸、镇国寺万佛殿每分°0.5寸、奉国寺大雄殿每分°0.65寸；这三个实例中，下昂斜度设计的基准三角形均为平出47分°，抬高21分°。在另几座《营造法式》之前的北方的双杪双下昂铺作——河北蓟县独乐寺观音阁上层（图24）、山西应县木塔一二层塔身（图25）、山西高平崇明寺（图26），虽然尚未进行三维激光扫描和数据取样归纳，但其下昂斜度均接近这个比例，所不同的是观音阁和木塔中标准斜度定在一二跳，昂广（非垂高）适合单材或足材，因此三四跳要增大许多。

图23 五台山佛光寺东大殿外檐铺作做法及其下昂部位示意图

图24 蓟县独乐寺观音阁外檐铺作做法及其下昂部位示意图

图25 应县木塔二层塔身外檐铺作做法及其下昂部位示意图

图26 高平崇明寺外檐铺作做法及其下昂部位示意图

在这些数据面前，我们足以浮想联翩。

也许，古人有一个算法表，是用不同的平出来抬高一足材，要么47分°，要么46分°，或者48分°；足材尺度要么21分°，要么20分°，或者22分°。

也许，古人只是偏爱这个47和21。而偏爱难道不需要原因吗？

只要再向前推演一步：47÷21≈2.238。这个比率可以让人想到√5，而√5≈2.236。虽然在简单整数比中38÷17≈2.235，更加接近√5取值，但是21仿佛具有更大的魅力。一旦有了√5的联想，下昂斜度设计就一下子变得简易了许多：

（1）并排画出两个标准正方形，边长为1足材；

（2）连接对角线，其长即为昂制平出。

再拓展一步，我们还可以联想到那根在宁波保国寺大殿（图27）、少林寺初祖庵大殿（图28）等建筑中出现的“五举”的下昂。暂时不引申论证，还是仅仅解释下算法自身的几何特点，将今天的几何认识与古代匠人可能的想法并置在一起，是否古今的理解略同呢？

图27 宁波保国寺外檐铺作做法及其下昂斜度示意图

图28 少林寺初祖庵外檐铺作做法及其下昂斜度示意图

“五举”的下昂真是具有一些“先天”的简明几何关系：平出为二，举高为一，斜边就是根五。更为有趣的是，在转角部位，斜昂的设计基准长为三。

那么“根五举”呢？在“五举”显得略陡的时候，简单地把“五举”的斜边变成平出，保持举高为一。那么转角部位的斜昂的设计基准长呢？是“根十一”，合3.32，约略是10/3。再有，如果用47和21作“根五举”，斜昂基准长就是69.7，可约作70。

（2）下昂广

在前文中总结了实测下昂广。那么，在下昂斜度关系假说的基础上延伸开来，两组下昂广数据之中掩藏着原设计者什么样的匠心呢？

首先，按照交接关系推算一下二昂组合在垂直方向上的高度到底应当是多少。参照上文推算和已经做过较深入研究的五台山佛光寺和义县奉国寺大殿外檐铺作下昂斜度，我们知道，下昂斜度由平出47分°、抬高21分°的直角三角形控制。做几则简单计算：

①从第二跳承跳斗斗口外楞至瓜子栱水平出=（17 -10）/2=3.5分°；
抬高=3.5×21/47=1.564≈1.6分°；

②上昂上皮与耍头上皮交会处自第二跳抬高=21+14=35分°（二材一栔）；

③二昂组合垂高=35-1.6=33.4分°。

接下来，看一下实测数据的情况（表28）。

表28 万佛殿外檐铺作慢栱长推算分析（单位：毫米）

测量对象与推算	头昂广	二昂广（及头昂单材部分）
均值	278.4	187.0
受力情况说明	受压受弯	受压受弯
变形情况说明	难以判断	难以判断
以47/21斜度计算垂高	305.1	204.9
折合分°	19.9	13.4
取整分°	20	13.4
吻合程度	99.69%	99.94%

表中实测均值推算得二昂广合计33.4分°。

这个推算完美得让人难以置信，然而将这种下昂垂高设计放在更大视野中考察，才可以引领我们逐步走进古代大木匠的内心世界：五台山佛光寺东大殿之下昂从第二瓜子栱外楞出（图29）、义县奉国寺大雄殿也是如此（图30）。此二例省去了从第二跳承跳斗斗口外楞至瓜子栱水平出的3.5分°，上昂上皮与耍头上皮交会处自第二跳抬高二材一栔，二昂组合垂高也正好是二材一栔，无须特别计算。

图29 五台山佛光寺东大殿下昂与承跳斗交接关系

图30 义县奉国寺大雄殿下昂与承跳斗交接关系

说得更远一点，广东肇庆梅庵大殿的下昂造中根本不估计下昂与二跳上承跳斗之间的承托逻辑，深深嵌入承跳斗斗欹（图31），在某种程度上只关注下昂斜度而放松了斗、昂关系。

图31 广东肇庆梅庵大殿下昂与承跳斗交接关系

那么是否可以说，比起上述三例中的下昂深入斗平的做法，在镇国寺大雄殿中的昂斗关系更追求细部的“构造美感”——或是更忠于“斗栱构造逻辑”呢？

是否可以说，为了追求这种“构造美感” 或是“斗栱构造逻辑”，镇国寺万佛殿的设计者——或者是他师从的工匠流派不惜为此付出了更多的计算？

是否可以说在“北方家族”的三个实例中，万佛殿代表的是更“年轻”的“改良派”，而奉国寺尽管建设年代稍晚，也当属于“保守派”呢？

细致入微的观察和测量帮助我们打开思想的翅膀。

梁架结构尺寸实测与分析

6.1

架道

首先，初步考察数据分布情况可以看出万佛殿屋架架道存在对称法则和转角对称关系，在这种对称法则和转角对称关系基础上，可以推导出一些基本架道的“等式关系”：

（1）正身架道1（柱心至下平槫）=进深架道1（柱心至下平槫）；

（2）正身架道2（下平槫至上平槫）=进深架道2（下平槫至上平槫）；

（3）正身架道1+正身架道2=进深架道1+进深架道2=次间开间；

（4）2×正身架道3（上平槫至脊槫）=进深明间。

进一步，利用三维激光扫描点云文件，可提取内槽东西缝之前后坡、东西山之南北丁栿之上共计8组数据，如表29。

表29 万佛殿架道推算（单位：毫米）

	架道1	架道2	架道3
东缝前	1722	1774	未及
东缝后	1721	未及	1849
西缝前	1765	1776	1833
西缝后	1744	1745	未及
东山南	1761	未及	未及
东山北	1761	1751	未及
西山南	1744	未及	未及
西山北	1763	1740	未及
均值	1747.6	1757.2	1841
最小值	1721	1740	1833
最大值	1765	1776	1849
方差	326.84	279.7	128
折合尺	5.7111	5.7425	6.0163
归整尺	5.75	5.75	6
吻合程度	99.32%	99.87%	99.73%
折合分°	114.22	114.85	120.33
归整分°	115	115	120
吻合程度	99.32%	99.87%	99.73%

可知，架道1=架道2=次间开间/2=5.75尺。

对照前文中推算出的材广厚和材份尺度，进一步考察架道均值，可知架道1（或架道2）水平长=115分°；架道3=120分°；撩风槫至柱心=95分°；前后撩风槫通深=890分°。

在这个115分°背后，还掩盖着这样一层深意——外檐铺作总出跳95分°，撩风槫至下平槫水平间距即为210分°，合1丈0尺5寸，便于用营造尺直接度量架道和椽长。与此相同的檐头架道设计还出现在始建于1200年的辽宁义县奉国寺大雄殿中——唯一的差别是，大雄殿1分°取值0.65寸，撩风槫至下平槫水平间距210分°合1丈3尺6寸5分，扣除外檐铺作总出跳，柱轴线至下平槫水平间距115分°合7尺4寸7分5，在进深架道（1丈6尺）分配上，约合7尺5寸，也是一种非常简明的算法。

6.2

出际

《营造法式》中记载“凡出际之制……六椽屋出三尺五寸至四尺”。实测万佛殿东西山出际——推算柱心线至搏风板内皮——分别为1385毫米和1411毫米，折合约4尺6寸，计92分°，吻合程度为99.32%。这个取值为115分°的0.8倍，与基本架道115分°之间存在简明的比例关系。考虑到歇山部位屋架架道为115分°，如此确定出际长或许是考虑到内外尺度关系。

再有，为了保证出际稳定，某次工程还添加立柱一根，下自山面补间铺作内二跳华栱栱身，上至脊槫底。

6.3

举折

（1）槫间高差实测

按照惯例，万佛殿各架道各槫间相对高度应直接测量，而测量部位应选择在各缝屋架承托各道槫的最贴近梁栿处，以减小槫子挠度对于高度测量的干扰。即使如此，在本例中影响直接测量结果的误差因素仍然存在，主要有二：①梁栿普遍存在挠度，使实测数据存在小于设计尺度的倾向；②襻间集中受压或倾斜，同样使实测数据存在小于设计尺度的倾向。

为了更加精确地考察、推算原始设计中举折做法，结合万佛殿屋架层叠严整、用材统一、历史修缮干扰小等特点，本次测绘针对其构造细部特征，归纳总结出以下关键距离，用于推算各槫间相对高度：

①各槫径尺度稳定，槫下替木高度同样稳定，脊槫、上平槫、下平槫之下替木广均为10分°；因此槫间高度差可以先行分别计算至替木底皮；

②如图32，撩风槫与下平槫之高差=3材3栔+间距A；

③如图33，下平槫与上平槫之高差=1材1栔+间距B；

④如图34，上平槫与脊槫之高差=间距C。

图32 撩风槫与下平槫高差关系示意图

图33 下平槫与上平槫高差关系示意图

图34 上平槫与脊槫高差关系示意图

分别测量东西缝前后坡、东西山前后缝之各槫高差，得到表30。

表30 万佛殿各槫高差中间距A、B、C归纳与推算（单位：毫米）

	A	B	C
东缝前	370	612	1245
东缝后	386	618	未及
西缝前	374	608	1254
西缝后	384	599	未及
东山南	391	587	未及
东山北	390	587	未及
西山南	385	601	未及
西山北	388	606	未及
平均值	383.5	602.3	1249.5
折合分°	25.07	39.36	81.67
归整分°	25	40	82
吻合程度	99.74%	98.41%	99.59%

再把各槫下替木高度相同之类的因素考虑进来，于是可以得到：

①撩风槫与下平槫之高差=88分°，其中上六椽栿、襻间栌斗平欹共垫高25分°；

②下平槫与上平槫之高差=61分°，其中四椽栿、驼峰、襻间栌斗平欹共垫高40分°；

③上平槫与脊槫之高差=82分°；

④总举高=231分°=11×21分°≈2×架道1（或架道2），合1丈1尺5寸5分；另参考，前后撩风槫总深=890分°，其1/4为225分°，合1丈1尺2寸5分，略小于总举高5分°，合2寸5分。

（2）举折做法试解

首先是“举屋之法”。严格地讲，万佛殿所反映的举屋方法并非《营造法式》中的举屋之法，而只是在“先量前后撩檐方心相去远近”，再按照“筒瓦厅堂”的规格，“四分中举起一分”。再考诸《营造法式》，有“又通以四分所得丈尺，每一尺加八分；若筒瓦廊屋及板瓦厅堂，每一尺加五分；或板瓦廊屋之类，每一尺加三分”之法，落实到万佛殿上，略似“又通以四分所得丈尺每一尺加三分”。事实上，万佛殿的总举高是近似四份举一份，前后撩风槫通深890分°之上举高取整231分°，合11足材。令我们感到惊奇的是，这个总举高分°值同样出现在五台山佛光寺东大殿中，或许反映出某些匠作算法流传的线索——尽管就此展开继承关系的研究还显得素材不足。

进而考察“折屋之法”。万佛殿架道不匀，分别为210分°、115分°和120分°，对照《营造法式》则属于“约度远近，随宜加减”之列。

如果深究各槫高差的成因，则可以按照取整至分°的精度考察上平槫和下平槫下折的尺度。参照图35计算可知，上平槫下折20分°，合1尺；下平槫再下折8分°，合4寸。对照《营造法式》折屋之法中“若椽数多，即逐缝取平，皆至撩檐方背，每缝并减上缝之半。如第一缝二尺，第二缝一尺，第三缝五寸，第四缝二寸五分之类”的方法，万佛殿采用的是一种原则相近、算法变通的做法。

图35 万佛殿举折算法示意图（单位：分°）

木材样本采集与检测

考虑到构件完整性，本次精细测绘选取略有破损处的松动部位，参考构件代表性、构造叠压深度关系，采集万佛殿木材样本5件，预期说明基本问题，不求信息完整全面。样本基础信息统计如表31。

表31 万佛殿木材样本基本描述

编号	位置	说明
01-T	西缝前上托脚	边材，构件广244厚149毫米
01-J	东立面北柱头铺作二跳上交互斗	靠内边材，构件尺度253×236×149毫米
02	东立面北柱头铺作栌斗	边材,构件尺度476×440×277毫米
03	东立面南柱头	边材，构件直径460毫米
04	南立面东次间下阑额上面	靠内边材，构件广267厚105毫米

7.1

木材种类

本次精细测绘采集万佛殿木材样本5份，全部预留部分样本用于材种鉴定。其中01-T、03、04三件样本结果一致，01-J、02二件样本用材一致。

（1）基本大木构件

01-T、03、04三件样本采集于基本大木构件，分别为托脚、立柱和阑额，鉴定结果如下：

中文名：硬木松

拉丁名：Pinus spp.

科别：松科 Pinaceae

微观鉴别要点：

生长轮明显，早材至晚材略急变。轴向薄壁组织缺如。射线管胞内壁有齿状加厚。具单列和纺锤形木射线。射线薄壁细胞与早材管胞间交叉场纹孔式为窗格状，稀松木型。具轴向和径向树脂道，其泌脂细胞壁薄。鉴定为松科双维管束松亚属的硬木松（Pinus spp.)。

（2）斗

01、02两件样本采集与万佛殿集中受力的斗——交互斗和栌斗，鉴定结果如下：

鉴定结果：
中文名：榆木
拉丁名：Ulmus spp.
科别：榆科 Ulmaceae

微观鉴别要点：

环孔材。早材导管肉眼下明显，宽1－3管孔，排列成明显早材带，含侵填体；早材至晚材急变；晚材导管甚小，多呈管孔团，与轴向薄壁细胞簇集呈弦向带状或波浪形排；单穿孔，导管间纹孔式互列，射线－导管间纹孔式类似管间纹孔式。螺纹加厚明显，仅存小导管和维管管胞。射线组织同形单列及多列。鉴定为榆科榆属的榆木(Ulmus spp.)。

（3）小节

硬木松是松属的一种，常见树种为油松、樟子松、高山松等。在晋中地区可能多是油松类或樟子松类。木材富含松脂，强度中等、耐腐，适作建筑用材。榆木在我国有23种，主要分布在华北、东北和西北等地区，其木材性质、质量区别不大。榆木木性坚韧，纹理清晰，较耐腐，硬度与强度较高，是木结构建筑的主要用材之一。

本测试结果可以初步看出万佛殿木结构中基本大木构件和斗类构件使用的木材不同。对比一些现有研究成果，可以发现万佛殿用材差异具有明确的目的性。我们已经知道：

①《太原晋祠圣母殿修缮工程报告》反映，大殿栌斗全部使用榆木，散斗多用榆木、间用落叶松，交互斗榆木、落叶松混用，其他大木基本构件全部使用落叶松；

②《晋东南古建筑木结构用材树种鉴定研究》中记载山西晋城青莲寺立柱用麻栎、梁用硬木松、枋榆木麻栎混用。

现在得到的万佛殿木材材种搭配与晋祠圣母殿的情况非常类似，基本构件采用强度中等的硬木松，而集中受力构件则采用硬度与强度较高的榆木。

7.2

木材样本C14年代判定

现有5件万佛殿木材样本全部送交美国BETA实验室进行碳同位素测年，结果显示，5件样本的木材死亡年代区间非常吻合，群体最大宽容区间为公元690至1010年。

表32 万佛殿木材样本碳同位素记年结果

样本编号	实测年龄	13C/12C	常规测年	双求和校准
01-T	1030 +/- 30 BP	-21.1 o/oo	1090 +/- 30 BP	Cal AD 890 to 1010 (Cal BP 1060 to 940)
04	1170 +/- 30 BP	-21.6 o/oo	1230 +/- 30 BP	Cal AD 690 to 880 (Cal BP 1260 to 1070)
03	1170 +/- 30 BP	-21.4 o/oo	1230 +/- 30 BP	Cal AD 690 to 880 (Cal BP 1260 to 1070)
02	1130 +/- 30 BP	-24.0 o/oo	1150 +/- 30 BP	Cal AD 780 to 980 (Cal BP 1160 to 970)
01-J	1110 +/- 30 BP	-22.0 o/oo	1160 +/- 30 BP	Cal AD 780 to 970 (Cal BP 1170 to 980)

对于上表中的检测结果，我们可以做出以下初步解读：

（1）万佛殿大木构件中最底层的构件——立柱、阑额所用木材相应取样部位木细胞（硬木松）死亡时间约在公元690年至880年之间（可能性≥95%），早于题记所反映的大殿营造年代公元963年；

（2）万佛殿大木构件斗栱中的深层构件——栌斗、交互斗所用木材相应取样部位木细胞（榆木）死亡时间约在公元780年至980年之间（可能性≥95%），早于题记所反映的大殿营造年代公元963年；

（3）万佛殿大木构件中较易受到修缮更换影响的上层构件——托脚所用木材相应取样部位木细胞（硬木松）死亡时间约在公元890年至1010年之间（可能性≥95%），其中值与题记所反映的大殿营造年代公元963年恰好相当。

结论与讨论

一般而言，研究成果具有不同的吻合水平，可以简单定义为结论、假说和猜想三个层次。那么，什么样的推算才被认为能够达到“推荐结论水平”？什么样的推算被认为仅仅属于“假说水平”呢？什么样的推算更加难于得到证实而只能归于“猜想水平”呢？

首先，任何推算的数据基础应当尽可能地追求数据的精度和覆盖率，应当详尽说明存在多少同类数据项，以及重复采集了多少数据。在以往的测绘要求中，一般会强调单个数据的准确程度，而测绘覆盖率的要求则相对薄弱。重复测量、大面积覆盖同类构件/构件关系尺度，不仅可以为数据分析提供坚实的基础，而且可以为探究后期更换构件、改造结构关系提供有益的线索。

进而，任何推算的数据前期处理应详尽说明同类数据的最大值、最小值和平均值，需要者应提供平方差等说明数据分布情况。根据笔者经验，均值在诸多计算中可以扮演重要的角色。

再有，在推算中我们必须注意到吻合程度。如前文已述，一般来讲：

（1）“推荐结论水平”的推算需要较严苛的吻合程度：分析构件之间的关系尺度时，要求吻合程度达到99%以上；分析单体构件自身尺度时，要求吻合程度达到97%左右即可；

（2）而“假说水平”的推算则需要达到以下条件——分析构件之间的关系尺度时，要求吻合程度达到97%以上；分析单体构件自身尺度时，要求吻合程度达到95%左右即可。

（3）未能达到“假说水平”的推算称为“猜想”。

最终，我们还必须清楚地认识到我们所做的推算不是简单地探究一把营造尺的长度和一套要么精确到半尺要么精确到寸的丈尺设计，而是要探究是否存在一种营造尺长和/或材份制度，可以满足建筑不同部位的简单算术比例关系和几何交接关系。对此可以参见傅熹年、何建中两位先生分别撰写的《中国古代城市规划、建筑群布局及建筑设计方法研究》《唐宋单体建筑之面阔与进深如何确定》《关于唐宋时期建筑物平面尺度用“分”还是用尺来表示的问题》《浅析〈中国古代城市规划、建筑群布局及建筑设计方法研究〉中的单层建筑设计方法》等著作、文章，公开讨论有关古建筑的尺度设计问题。

当前一些学者注意到，某地域、某时代还使用鲁班尺、压白尺等不同的度量单位，作为营造尺的引申，也有学者提出，可能存在某种“扩大模数”，甚至有人提出一种基于营造尺长的过渡度量——偏离用材的“基本模数”，并据此构成建筑主体比例关系。尽管《鲁班经》之类的史料中明确提出“鲁班尺”用于“门户”、“宅门”、“室院”尺度的吉凶，但是鉴于目前掌握的古建筑实测资料，我们无法简单肯定或者质疑这些特殊用尺的使用情况。而回答营造尺之外占蓍类用尺使用情况的问题之前，必须先考察营造尺是否适用并回答古人如何选择、确定丈尺数的问题。只有在清晰地证实营造尺是否适用和如何使用的前提下，拓展讨论才会变得更有意义。不妨把本文的假说作为探讨的第一步走向精细测绘、深入解读的尝试。言归正传，笔者将建立在营造尺基础上的结构关系归结为以下五个条件方程：

①是否存在一把营造尺，使柱头平面的丈尺符合某一种简明的设计？——一般情况下精确度为半尺，在一些情况下平面设计是结合屋架架道进行的，因此平面丈尺会精确到寸，使得屋架架道设计更为简明。

②如果柱头平面采用精确到半尺的设计，是否还是同一把营造尺，使屋架尺度符合某一种简明的设计？

③是否仍然是同一把营造尺，与斗栱材份制度之间存在简明的对应关系？

④以上述材份制度为基础，斗栱各部分基本组成是否同样符合某一种简明的设计？

⑤在早期建筑下昂造或晚期建筑溜金斗栱中，下昂/挑斡的斜度是否符合某一种简明的设计？

正是出于上述五个条件方程，笔者的研究倾向于选择带有下昂的早期建筑。这种在空间中呈倾斜姿态的构件，自然地为简单的正交体系带来了复杂的约束条件，使得与之相关的正交构件存在某种简明做法，而下昂斜度的设计也应符合某种简明算法。一旦这种算术/几何关系为我们所读通，其他的构造和尺度关系便往往能够迎刃而解。

推算基础要求已经在上文各个小节中全面反映，万佛殿各项主要数据均值与推算结果之间的吻合程度达到很高的水平，形成一套“推荐结论”、一条“假说”、一条“猜想”。

“推荐结论”的推算吻合程度标准罗列如下。

①在推算过程中，柱头平面、架道、出际、斗栱出跳与足材广的推算吻合程度全部达到99%以上；

②屋架举高的吻合程度分别达到99.74%、98.41%、99.59%；

③各类栱、昂之长、广、厚普遍达到99%至98%的吻合程度，个别略低，仍然显著高于97%；

④各类斗之细节尺度吻合程度偏低，最高达到99%以上，最低处为散斗斗平，仅有87.43%，可以认为后者受到了后期更换和集中受压形变的影响；但包括此最低值在内的各类斗所有吻合程度的均值达到96.58%；

⑤栿、槫、额、角梁、托脚、叉手、蜀柱、襻间、替木各类构件吻合程度较高，最低者出现在蜀柱进深，为95.32%，包括此最低值在内的各类构件吻合程度均值为98.59%。

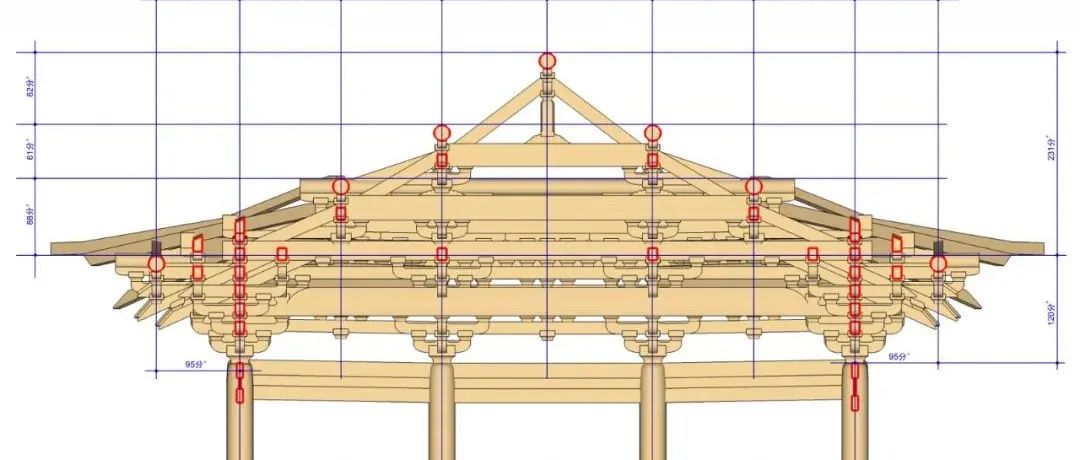
综上所述，按照五个条件方程整理万佛殿大木设计的基本算法，得到的以下推算达到“推荐结论水平”（图36）：

图36 万佛殿木结构设计示意图

①万佛殿木结构主体构件用材取材年代约为公元9世纪至10世纪，与殿内最早题记年代相吻合，可以做出大殿建于公元963年的判断。

②在未发现实测数据存在特异值的情况下，按照统计后的均值计算，万佛殿用营造尺长306毫米，万佛殿用营造尺适用范围为建筑主体的各个部位，且结构关系尺寸简明——柱头平面丈尺设计精确到半尺：面阔方向，明间14尺5寸，东西次间11尺5寸；进深方向，当心间12尺，前后次间11尺5寸。

③在架道设计上，下平槫均分前后进深的11尺5寸，为每架道5尺7寸5分；脊槫均分当心进深的12尺，为每架道6尺；屋架柱心内的前后两架与斗栱总出跳份数还存在更深层的配合设计。

④在剔除个别实测数据特异值的情况下，按照统计后的均值计算，万佛殿外檐铺作以材厚为基准分为10分°，每分°0.5寸。

⑤在剔除个别实测数据特异值的情况下，按照统计后的均值计算，外檐铺作单材广并不遵循《营造法式》规定的15分°，而更倾向于14分°；第一二总出跳出48分°；第三四总出跳平出47分°。

⑥针对下昂设计，在剔除个别实测数据特异值的情况下，结合现状构造交接，并按照统计后的均值计算，可以判断第二根下昂上皮过耍头上皮与第二跳慢栱上皮的交点，因此第三四总出跳决定下昂斜度，下昂斜度设计的基准三角形均为平出47分°，抬高21分，与已知的佛光寺东大殿、奉国寺大雄殿的下昂斜度设计相同。

通过上述五个条件方程的建立，我们不仅确认、验证了306毫米长的营造尺、厘清的平面、架道、斗栱设计，还可以进一步利用推算结论对结构变形相对最剧烈、最易受到历史改造影响的屋架举折进行摸索推算。

此外，前文中关于角柱生起的陈述，仅可作为一种猜测，尚无法达到前文规定的“假说水平”；前文中的计算还表明，万佛殿屋架在前后撩风槫通深890分°之上举高取整231分°，合11足材，虽然推算吻合程度基本符合99%的“推荐结论水平”要求，但是考虑到目前尚不能全面鉴定木材年龄的情况，无法更详尽地推知构件更换、修改的历史，因此本文将此作为“假说水平”的论断。